Post by Nicolas RémondFlûte, oui, en effet, la question était mal posée.
La question serait plutôt, dans un repère orthonormé cartésien qui
va bien, comment trouve-t-on, efficacement, l'angle entre deux vecteurs
O-M1 O-M2 à 2*Pi près.
En fait, existe-t-il une méthode plus rapide que de récrire les
vecteurs dans le plan O-M1-M2 et de prendre un l'acos du produit
scalaire et le signe ensuite par le signe du déterminant?
Cette projection préalable dans le plan (dans la direction de plan)
O-M1-M2, est une opération superflue. Tu procèdes directement au
produit scalaire par les coordonnées cartésiennes.
C'est simplifié, puisqu'en cartésiennes orthonormées, le tenseur
métrique se réduit au tenseur unitaire, multiplié par le carré de
l'unité de longueur.
Tandis que tu t'es introduit un faux problème parasitaire avec cette
projection sur le plan O-M1-M2 : Supposant défini (mais sacrebleu,
comment ?) une orientation en rotation sur ce plan O-M1-M2, quel est
alors le signe de l'angle orienté (M1,M2) ? Sauf que rien au départ ne
te permettait de choisir quel sens de rotation est le sens positif sur
ce plan O-M1-M2. C'est totalement arbitraire, sauf au voisinage
immédiat d'un des trois plans de base de ton repère, en supposant
toutefois que chacun soit défini en sens de rotation par l'ordre
circulaire des trois vecteurs de base i -> j -> k -> i. Tu ne peux pas
rendre connexes ces trois orientations, pour en faire une orientation
générale de la rotation dans R^3.
Résumons : il n'existe pas de signe, dans l'espace R^3, pour l'angle
entre deux vecteurs. Alors que si dans un plan, on a défini le sens de
rotation positif, alors oui, on peut définir l'angle orienté.
Hélas, les différentes notions empilées sous le seul vocable de
"angle", sont un des plus noirs bordels de l'enseignement des
mathématiques. J'ai publié la carte des relations sémantiques, reliant
les différentes sortes d'"angles" connus des élèves de seconde :
Loading Image...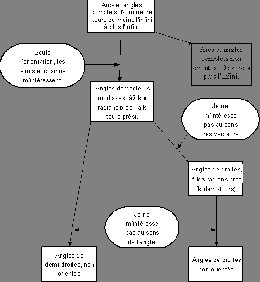
Cela n'inclut donc évidemment pas les "angles" entre spinneurs.
Cela dans la seconde partie de l'article *La persistance de schèmes
infantiles dans l’enseignement des mathématiques et de la physique. Et
pour devenir une science ?*
Ici, pour ton problème, tu commences à être confronté à un problème du
genre : quel est l'opérateur qui me fait passer du vecteur M1 au
vecteur M2 ?
Si tu confonds le vecteur avec ses cooordonnées (ce qui est une faute
professionnelle standardisée depuis le 19e siècle), alors la réponse
est que cet opérateur est une matrice : celle qui multipliant les
coordonnées de M1, donne les coordonnées de M2.
Si tu es plus rigoureux, que tu concèdes à M1 et M2 une signification
physique intrinsèque, indépendante du système de coordonnées, alors
l'opérateur de passage est un tenseur, quotient de M2 par M1. Il est
autorisé à avoir une dimension physique, des unités physiques dans ses
coordonnées. Un tenseur est un être géométrique, applicable à la
physique en tant que "descripteur de ...", qui a un caractère de
réalité indépendant de l'observateur, et du repère de l'observateur.
--
La science se distingue de tous les autres modes de transmission des
connaissances, par une croyance de base : nous croyons que les experts
sont faillibles, que les connaissances transmises peuvent contenir
toutes sortes de fables et d’erreurs, et qu’il faut prendre la
peine de vérifier, par des expériences.
-- Jacques Lavau (retirer les anti et les spam pour le courriel)
http://lavaujac.club.fr