Olivier Miakinen
2016-03-13 21:50:29 UTC
[diapublication avec fr.sci.maths, suivi vers
fr.education.entraide.maths seul]
Bonjour,
Je suis tombé sur un exercice intéressant dans le livre d'exercices
de mon fils qui est en 5e.
Voir la figure suivante :
<Loading Image...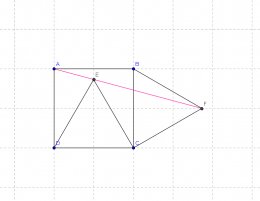 >.
>.
Partant d'un carré ABCD, on a tracé un triangle équilatéral CDE (E à
l'intérieur du carré) et un triangle équilatéral BCF (F à l'extérieur
du carré).
Les points A, E et F semblent alignés, et la question est de savoir
s'ils le sont réellement.
++++++++++++++++++++++++++++++++++++++++++++++++++++++
Comme j'ai lu les conseils d'utilisation de ce groupe, je commence
par montrer que j'ai cherché...
En fait, on peut facilement prouver que les points sont alignés
en calculant d'une part la tangente de l'angle EAB (qui vaut
2 - racine(3)) et d'autre part celle de l'angle FAB (qui vaut
l'inverse de 2 + racine(3)).
Vu que (2 - racine(3)).(2 + racine(3)) vaut 1, les deux tangentes
sont égales, et donc les angles sont égaux.
Le problème, c'est que ma solution n'est pas à la portée des
élèves de 5e, et j'aimerais bien savoir quelle solution serait
à leur portée.
++++++++++++++++++++++++++++++++++++++++++++++++++++++
Histoire de trouver l'inspiration, j'ai rajouté quelques points
et droites ainsi qu'un cercle à la figure d'origine :
<Loading Image...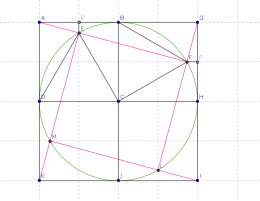 >.
>.
Je me rends bien compte qu'il suffit de remarquer que le
triangle rectangle AGF est semblable au triangle GFF' et
donc au triangle AEE', mais ça me semble encore un peu trop
compliqué pour des 5e. Je me trompe ?
Si vous avez une meilleure idée, je veux bien quelques
indications plutôt qu'une solution complète, du moins si
c'est possible.
[Rappel : j'ai mis le suivi vers feem seul]
Cordialement,
fr.education.entraide.maths seul]
Bonjour,
Je suis tombé sur un exercice intéressant dans le livre d'exercices
de mon fils qui est en 5e.
Voir la figure suivante :
<Loading Image...
Partant d'un carré ABCD, on a tracé un triangle équilatéral CDE (E à
l'intérieur du carré) et un triangle équilatéral BCF (F à l'extérieur
du carré).
Les points A, E et F semblent alignés, et la question est de savoir
s'ils le sont réellement.
++++++++++++++++++++++++++++++++++++++++++++++++++++++
Comme j'ai lu les conseils d'utilisation de ce groupe, je commence
par montrer que j'ai cherché...
En fait, on peut facilement prouver que les points sont alignés
en calculant d'une part la tangente de l'angle EAB (qui vaut
2 - racine(3)) et d'autre part celle de l'angle FAB (qui vaut
l'inverse de 2 + racine(3)).
Vu que (2 - racine(3)).(2 + racine(3)) vaut 1, les deux tangentes
sont égales, et donc les angles sont égaux.
Le problème, c'est que ma solution n'est pas à la portée des
élèves de 5e, et j'aimerais bien savoir quelle solution serait
à leur portée.
++++++++++++++++++++++++++++++++++++++++++++++++++++++
Histoire de trouver l'inspiration, j'ai rajouté quelques points
et droites ainsi qu'un cercle à la figure d'origine :
<Loading Image...
Je me rends bien compte qu'il suffit de remarquer que le
triangle rectangle AGF est semblable au triangle GFF' et
donc au triangle AEE', mais ça me semble encore un peu trop
compliqué pour des 5e. Je me trompe ?
Si vous avez une meilleure idée, je veux bien quelques
indications plutôt qu'une solution complète, du moins si
c'est possible.
[Rappel : j'ai mis le suivi vers feem seul]
Cordialement,
--
Olivier Miakinen
« Au fond, diviser par zéro revient à unifier la Mécanique Quantique
et la Relativité Générale. » -- M.A. le 7/3/2016 dans fr.sci.maths
Olivier Miakinen
« Au fond, diviser par zéro revient à unifier la Mécanique Quantique
et la Relativité Générale. » -- M.A. le 7/3/2016 dans fr.sci.maths